10-30-2009
|
 |
|
|
تاریخ عضویت: Aug 2009
نوشته ها: 16,247
سپاسها: : 9,677
9,666 سپاس در 4,139 نوشته ایشان در یکماه اخیر
|
|
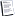نظریه گراف
نظریه گراف
- تعریف
- انواع گراف‌ها
- گراف‌ها و ساختار داده‌ها
- مسایل گراف
- الگوریتم‌های مهم
- همچنین ببینید
- پیوندهای خارجی
در ریاضی و علوم کامپیوتر، نظریه گرافعلمی است که به مطالعه گراف‌ها می‌پردازد.گراف مجموعه‌ای از راس‌هاست که بوسیله یال‌ها به هم وصل شدهاند.به عبارت ساده‌تر به مجموعه‌ای از نقاط که بوسیله خطوط به هم وصل شدهاند، گراف گویند. مفهوم گراف در سال 1736 توسط اویلر و با طرح راه‌حلی برای مساله پل konigsberg ارائه شد و به تدریج توسعه یافت.گراف‌ها امروزه کاربرد زیادی در علوم دارند. از گراف‌ها در شبکه‌ها،طراحی مدارهای الکتریکی, اصلاح هندسی خیابان‌ها برای حل مشکل ترافیک،و.... استفاده میشود.
تعریف
فرض کنید V یک مجموعه ناتهی و E زیرمجموعه‌ای از باشد در این صورت زوج را یک گراف می نامند.V را مجموعه راس ها و E را مجموعه یال ها می گویند. اگر ترتیب قرار گرفتن راس ها در مجموعه E مهم باشد،گراف را گراف جهت‌دار می گویند و یال از راس به سمت راس را به صورت نشان می‌دهند.در غیر این صورت گراف را بدون جهت می‌نامند و یال بین راس های و با نماد نشان می‌دهند.
تعداد راس های یک گراف را مرتبه و تعداد یال های آن را اندازه گراف می نامیم.
در شکل روبرو گرافی را با شش راس و هفت یال مشاهده می کنیم
انواع گراف‌ها
گراف‌ها دارای انواع متعددی هستند که به برخی از آنها اشاره می‌کنیم: - گراف همبند
- گراف ناهمبند
- گراف کامل
- گراف اویلری
- گراف همیلتونی
- گراف درختی
- گراف مسطح
- گراف دو بخشی
- گراف چندبخشی
- گراف k-مکعب
- گراف چرخ
- گراف ستاره‌ای
- گراف بازه‌ای
- گراف اشتراکی
- گراف منظم
- گراف جهت‌دار
گراف‌ها و ساختار داده‌ها
هر گراف را می‌توان با یک ماتریس نمایش داد ، که به آن ماتریس مجاورت گراف گویند. در این روش از آرایه هااستفاده می‌کنیم.این ماتریس به تعداد راس‌های گراف دارای سطر و ستون است.وعدد 1 نشان دهنده وجود یک یال بین دو راس و عدد 0 نشان دهنده عدم وجود ارتباط بین دو راس است.یعنی ماتریس ما شامل دو عدد صفر و یک است. با استفاده از این ماتریس می‌توان رئوسی را که با یک راس در ارتباط‌اند و نیز رئوسی را که با هیچ راس دیگری ارتباط ندارند رامشخص کرد.
مسایل گراف
- تئوری رنگ آمیزی
- قضیه چهار رنگ
- مسائل حل نشده در رنگ آمیزی
- مسائل موجود در زمینه مسیر
- Minimum spanning tree
- درخت steiner
- مساله کوتاهترین مسیر
- مساله پستچی چینی
- مساله فروشنده دوره گرد
الگوریتم‌های مهم
- الگوریتم kruskal
- الگوریتم prim
- الگوریتم کوتاهترین مسیر
__________________
زمستان نیز رفت اما بهارانی نمی بینم
بر این تکرارِ در تکرار پایانی نمی بینم
به دنبال خودم چون گردبادی خسته می گردم
ولی از خویش جز گَردی به دامانی نمی بینم
چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت!
که غیر از مرگ، گردن بند ارزانی نمی بینم
زمین از دلبران خالی است یا من چشم ودل سیرم؟
که می گردم ولی زلف پریشانی نمی بینم
خدایا عشق درمانی به غیر از مرگ می خواهد
که من می میرم از این درد و درمانی نمی بینم
استاد فاضل نظری |
|
جای تبلیغات شما اینجا خالیست با ما تماس بگیرید
|
|