
|
|
|||||||
| فنی و مهندسی در این زیر تالار به بحث و گفتگو در مورد رشته های فنی و مهندسی پرداخته میشود |
|
|
ابزارهای موضوع | نحوه نمایش |
|
#11
|
||||
|
||||
اعمال جبری روی توابع
__________________
زمستان نیز رفت اما بهارانی نمی بینم بر این تکرارِ در تکرار پایانی نمی بینم به دنبال خودم چون گردبادی خسته می گردم ولی از خویش جز گَردی به دامانی نمی بینم چه بر ما رفته است ای عمر؟ ای یاقوت بی قیمت! که غیر از مرگ، گردن بند ارزانی نمی بینم زمین از دلبران خالی است یا من چشم ودل سیرم؟ که می گردم ولی زلف پریشانی نمی بینم خدایا عشق درمانی به غیر از مرگ می خواهد که من می میرم از این درد و درمانی نمی بینم استاد فاضل نظری |
| کاربران در حال دیدن موضوع: 1 نفر (0 عضو و 1 مهمان) | |
|
|
اکنون ساعت 07:03 AM برپایه ساعت جهانی (GMT - گرینویچ) +3.5 می باشد.





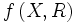
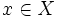
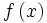
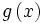
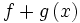
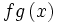
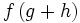
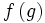
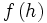
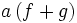
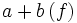
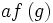
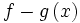
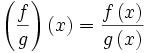
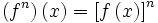
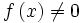
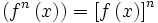
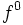
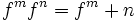
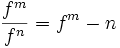
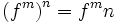
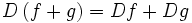

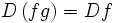
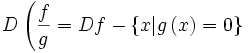
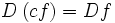



 حالت رشته ای
حالت رشته ای